Lab sheet 8: Central Limit Theorem

Let $X_1,X_2,\dots$ be a sequence of independent, identically distributed random variables, each with mean $\mu$ and variance $\sigma^2$ . Then the distribution of $\dfrac{X_1+X_2+\dots+X_n-n\mu}{\sigma\sqrt{n}}$ tends to the standard normal as $n\to \infty$ . That is, $P\left(\dfrac{X_1+X_2+\dots+X_n-n\mu}{\sigma\sqrt{n}}\leq a \right)\to \dfrac{1}{\sqrt{2\pi}} \int_{-\infty}^{a}e^{-x^2/2}dx$ as $n\to\infty$ .

In other words, the central limit theorem tells us that if the population distribution has mean $\mu$ and standard deviation $\sigma$ , then the sampling distribution of the mean also has mean $\mu$ , and the standard error of the mean is $\mbox{S} = \frac{\sigma}{ \sqrt{n} }.$ We can see this experimentally. We will consider some known distribution and do the experiments.

Normal distribution

# mean and standard deviation of normal distribution
m <- 0
s <- 1
# folowing fuction is written to show the histogram plot of sample mean.
mean.histplot <- function(n,N=50000) {
  # n - sample size
    X <- matrix(rnorm(n*N,m,s),n,N)
    X <- colMeans(X)
    # generate histogram
    hist( X, breaks="Sturges", border="white", freq=FALSE,
            col="blue",
            xlab="Sample mean", ylab="", xlim=c(-3.5,3.5),
            main=paste("Sample size =",n), axes=FALSE,
            font.main=1
        )
    box()
    axis(1)
    # plot N(mu,sigma/sqrt(n))
    lines( x <- seq(-3.0,3.0,.01), dnorm(x,m,s/sqrt(n)), 
    lwd=2, col="black", type="l"
    )
}

mean.histplot(1)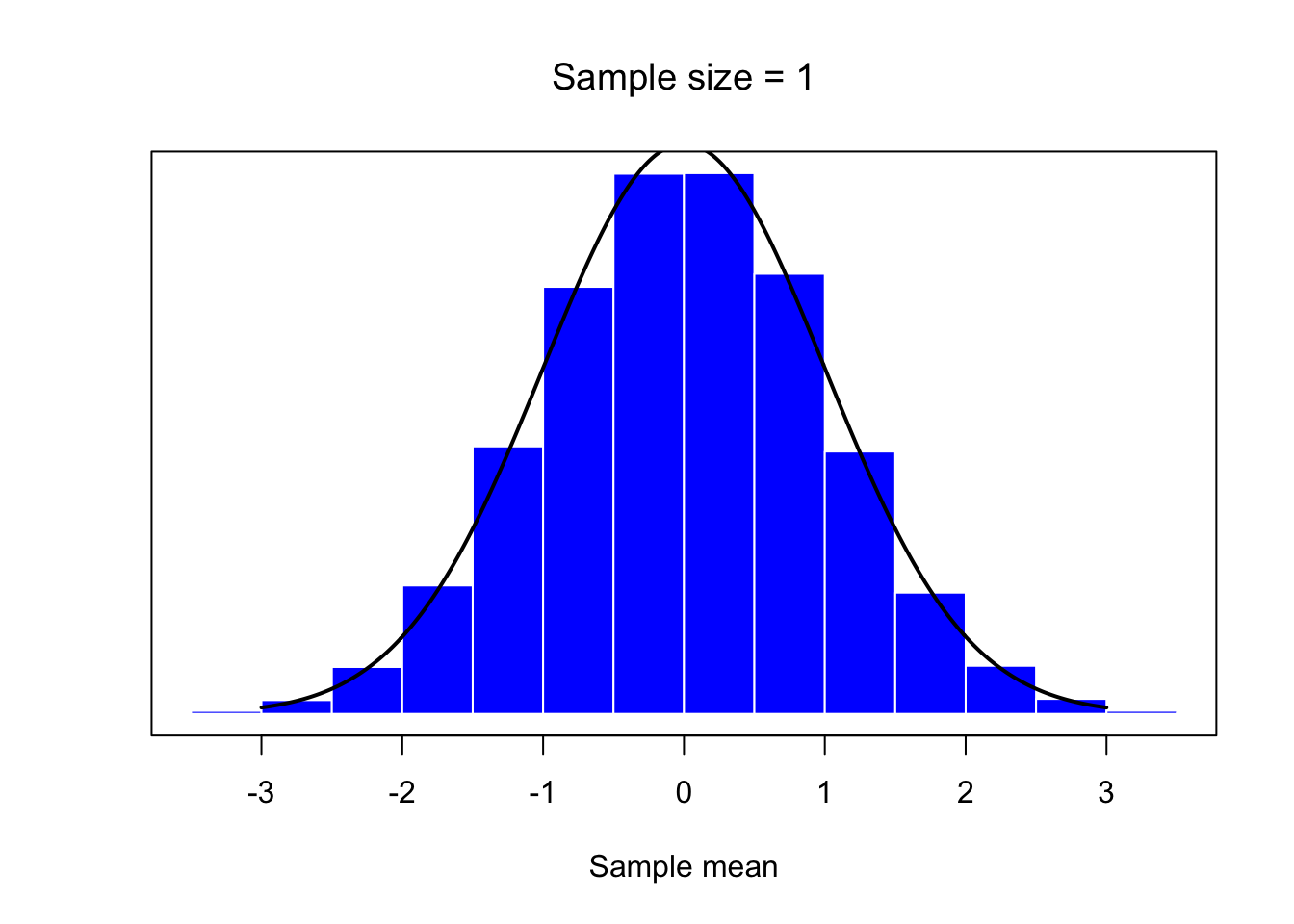

mean.histplot(4)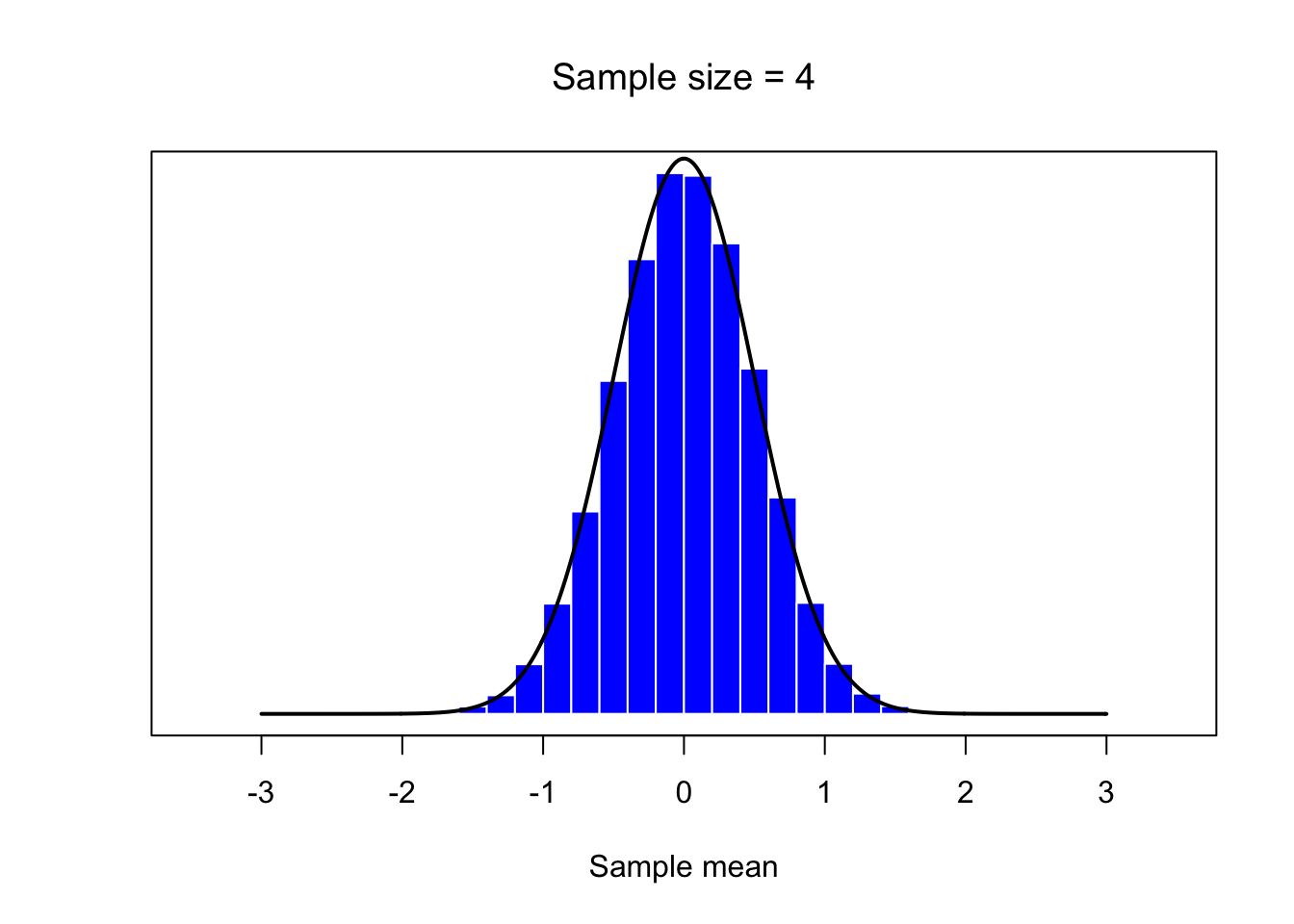

mean.histplot(30)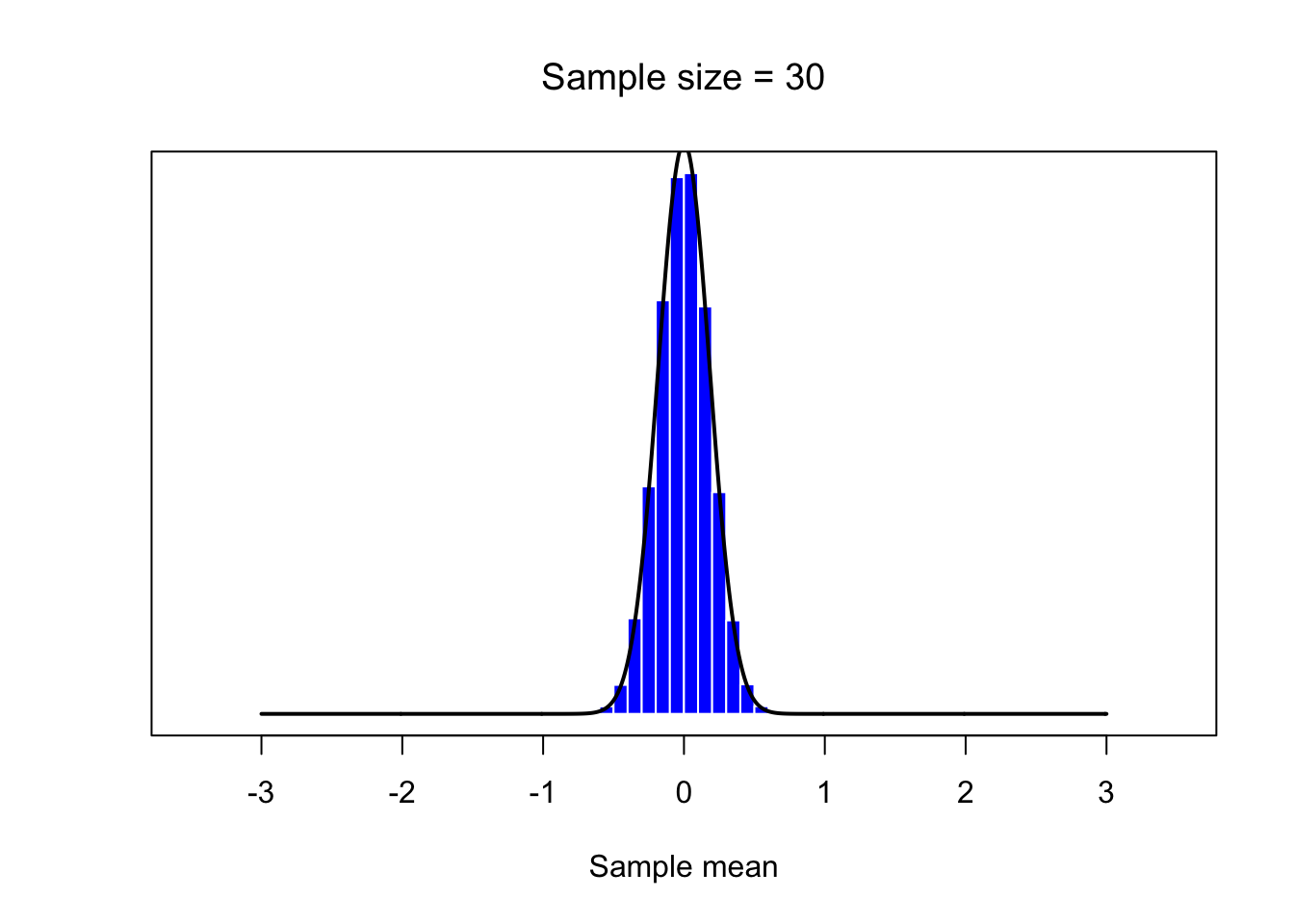

Poission distribution

# Lambda, mean and standard deviation 
L<-2
m <- L
s <- sqrt(L)
    
# define function to draw a plot
mean.histplot <- function(n,N=50000) {
  # n - sample size
    X <- matrix(rpois(n*N,L),n,N)
    X <- colMeans(X)
    # generate histogram
    hist( X, breaks="Sturges", border="white", freq=FALSE,
            col="blue",
            xlab="Sample mean", ylab="",
            main=paste("Sample size =",n), axes=FALSE,
            font.main=1
        )
    box()
    axis(1)
    # plot N(mu,sigma/sqrt(n))
    lines( x <- seq(-30.0,30.0,.01), dnorm(x,m,s/sqrt(n)), 
    lwd=2, col="black", type="l"
    )
}

mean.histplot(1)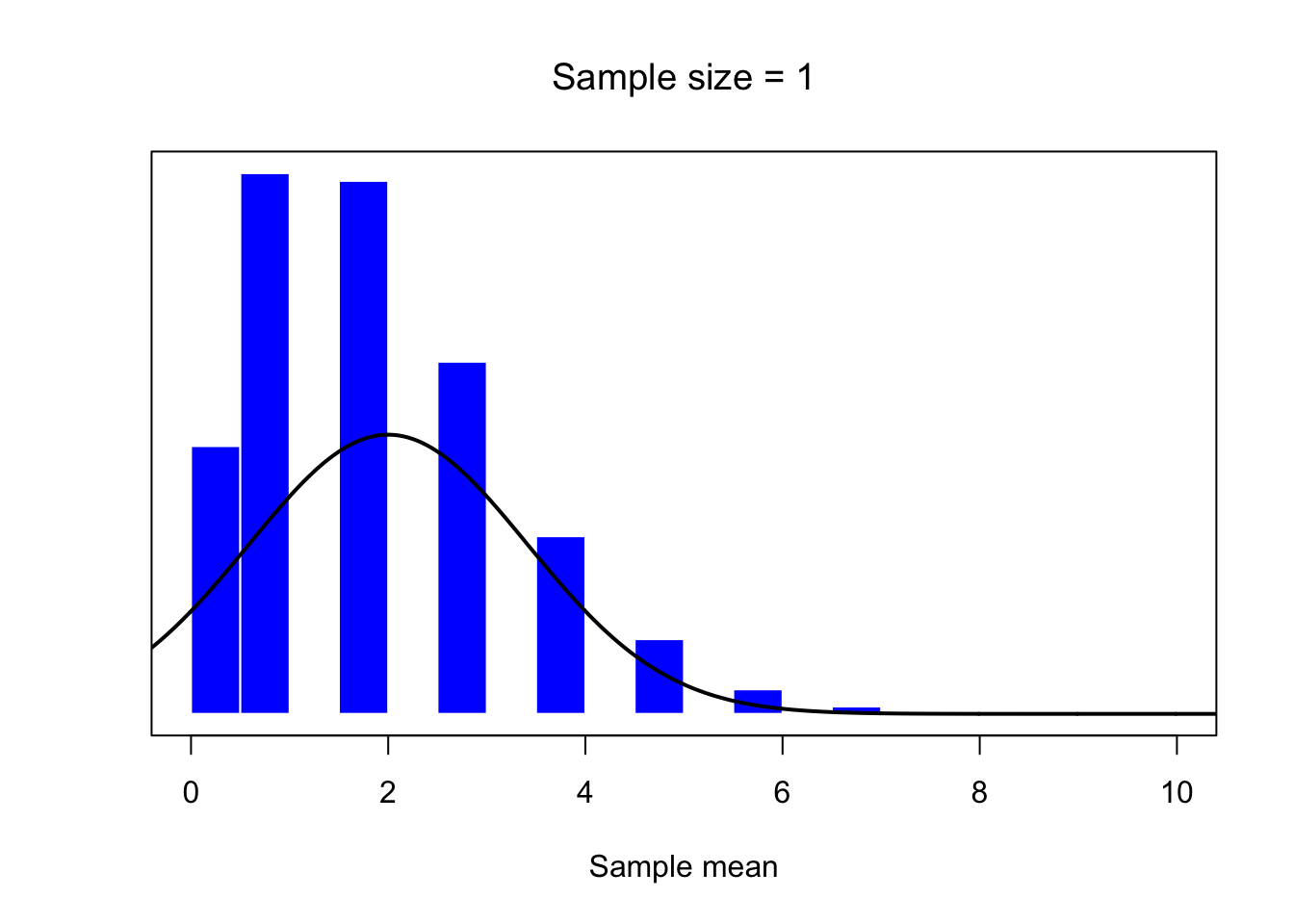

mean.histplot(4)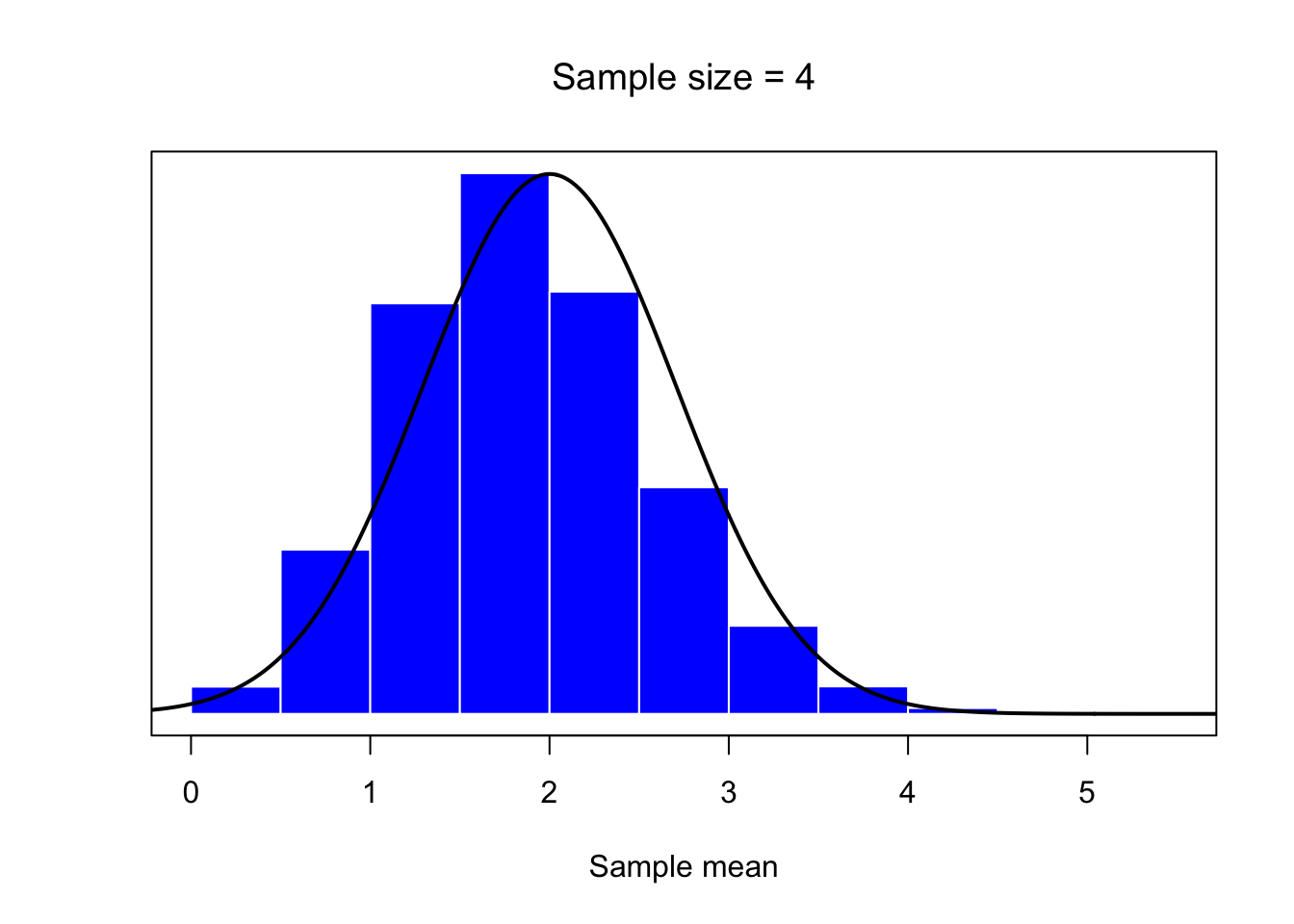

mean.histplot(30)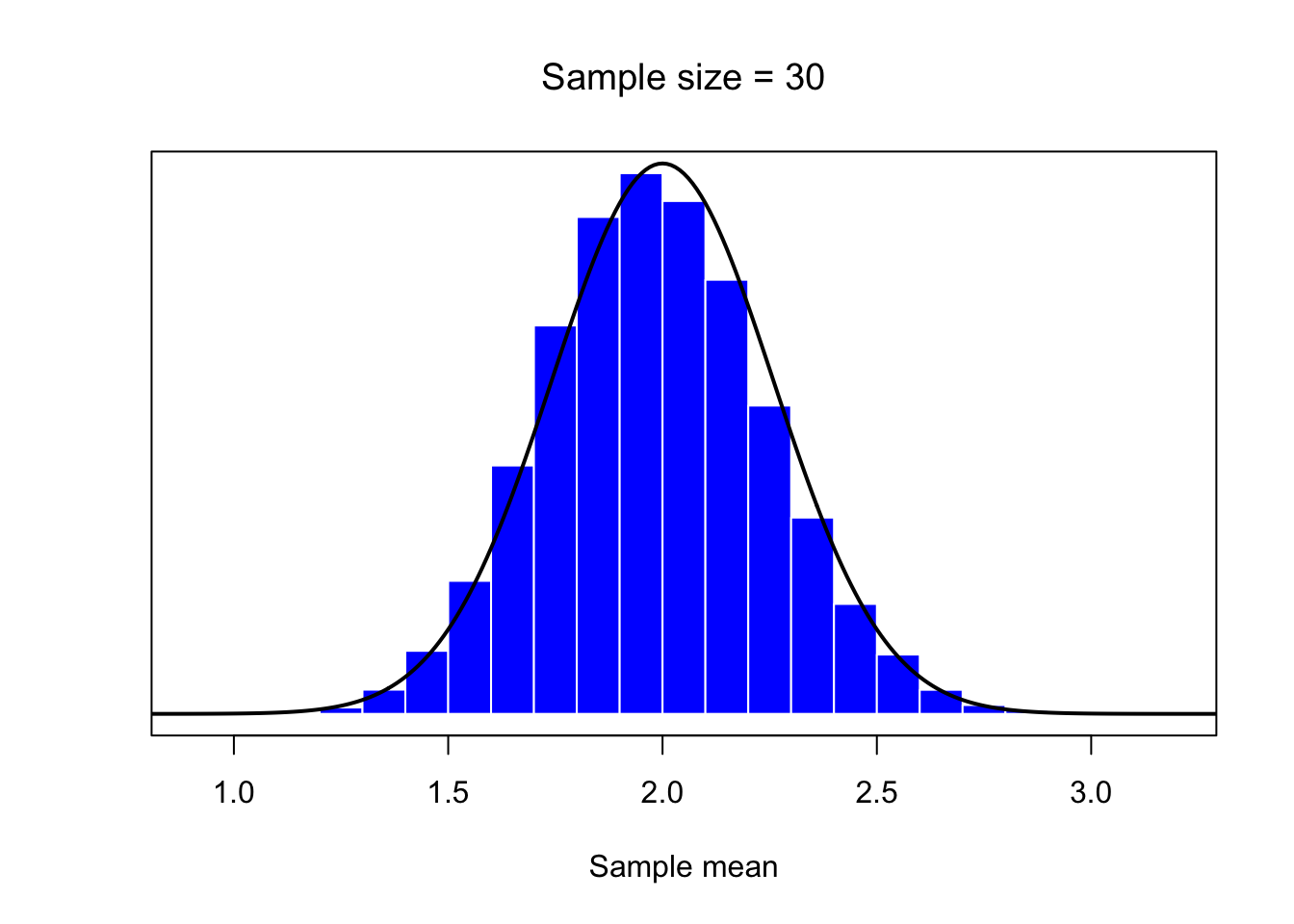

Exponential distribution

# Lambda, mean and standard deviation 
L<-3.5
m <- 1/L
s <- 1/L
# define function to draw a plot
mean.histplot <- function(n,N=50000) {
  # n - sample size
    X <- matrix(rexp(n*N,rate=L),n,N)
    X <- colMeans(X)
    # generate histogram
    hist( X, breaks="Sturges", border="white", freq=FALSE,
            col="blue",
            xlab="Sample mean", ylab="",
            main=paste("Sample size =",n), axes=FALSE,
            font.main=1
        )
    box()
    axis(1)
    # plot N(mu,sigma/sqrt(n))
    lines( x <- seq(-30.0,30.0,.01), dnorm(x,m,s/sqrt(n)), 
    lwd=2, col="black", type="l"
    )
}
mean.histplot(1)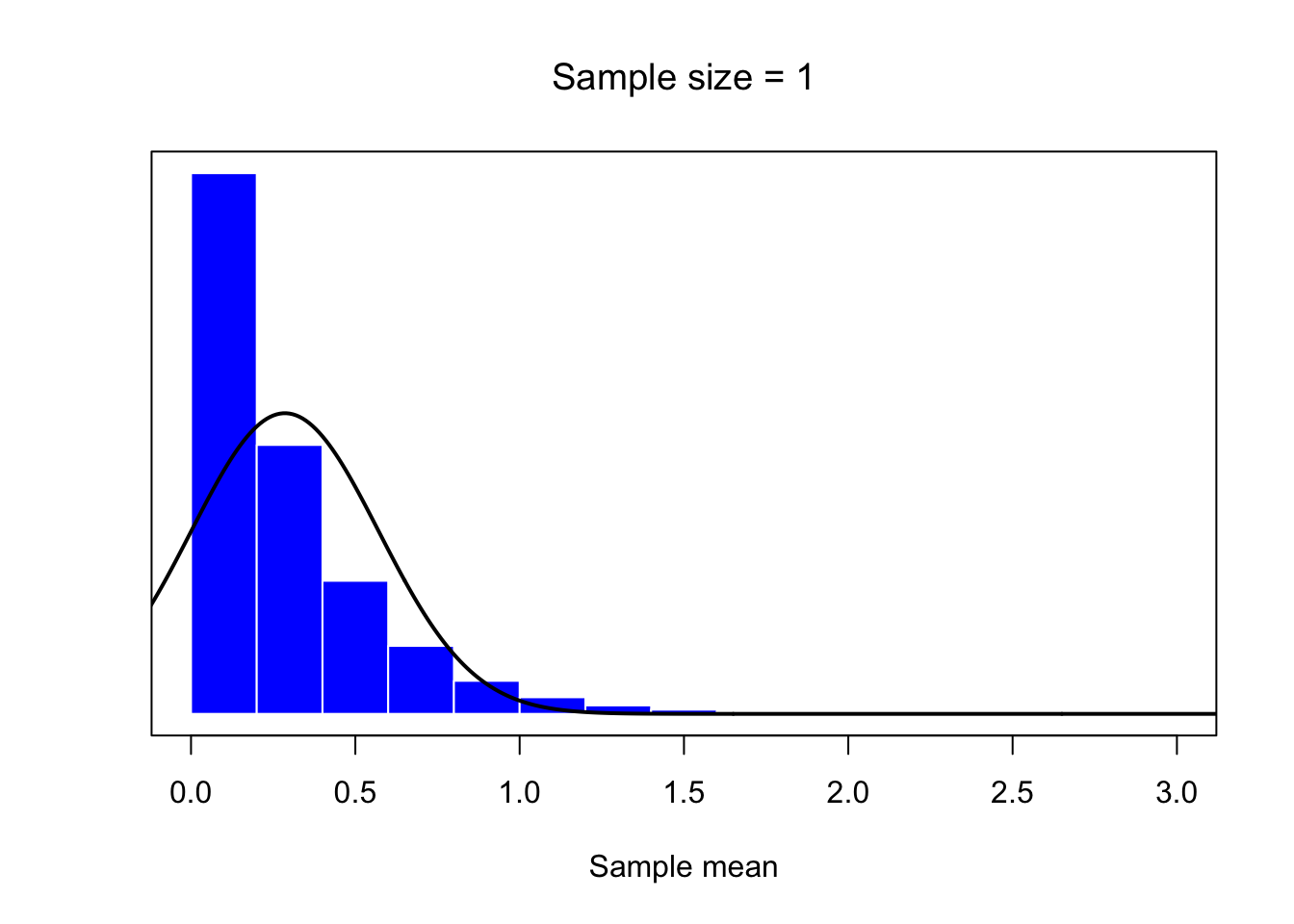

mean.histplot(4)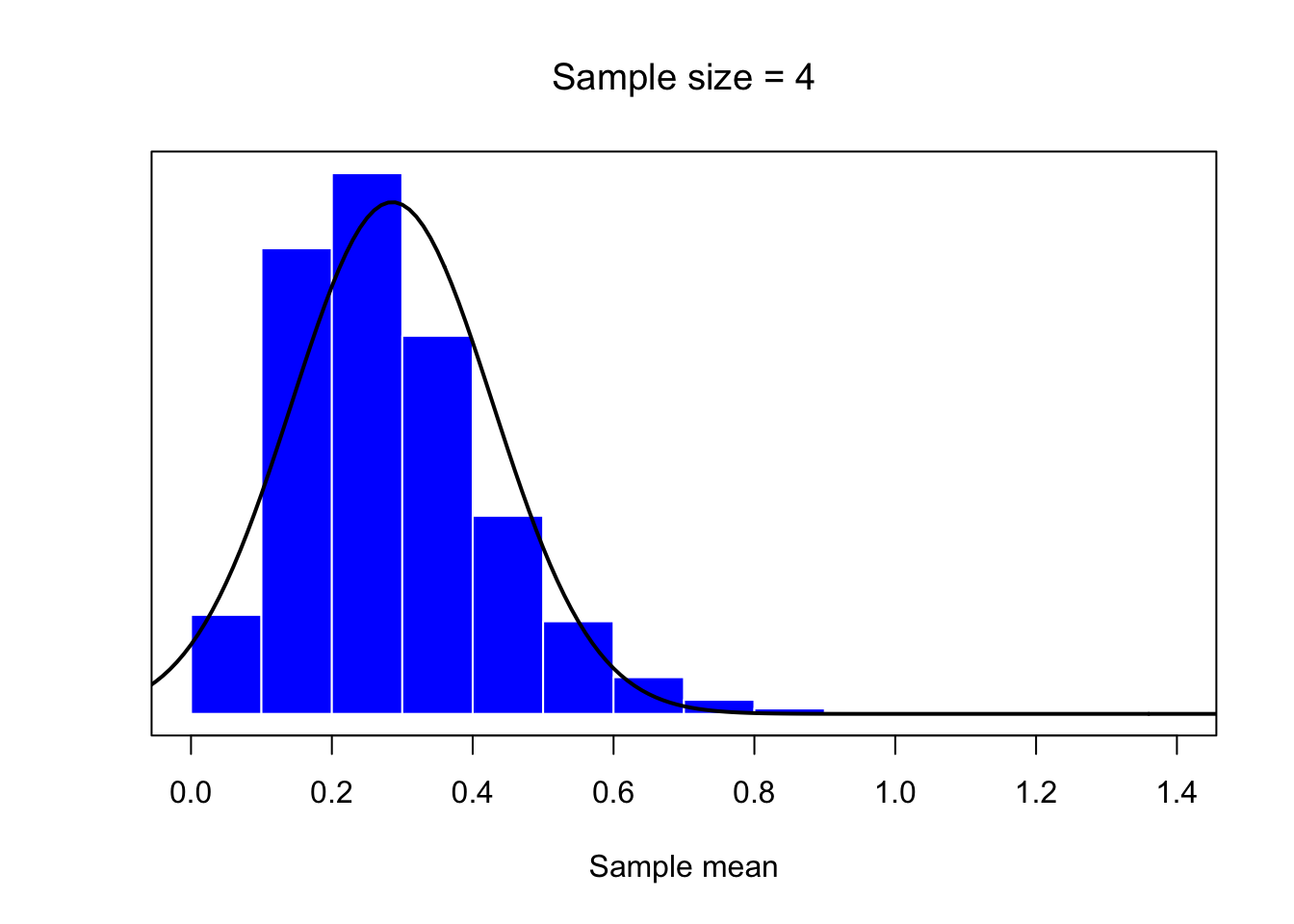

mean.histplot(30)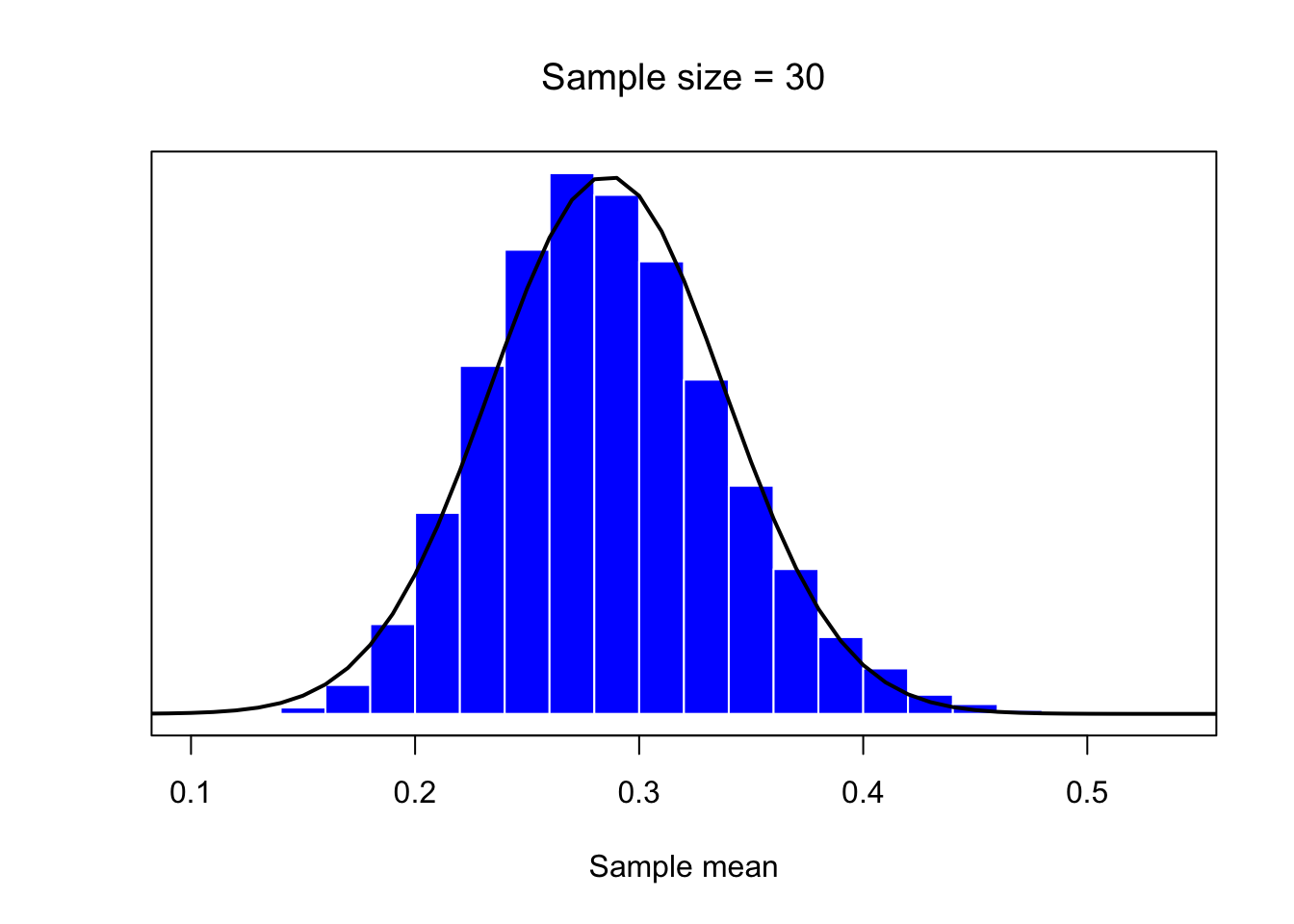

Binomial distribution

# parameters
n1<- 10
p <- 0.7
q <- 1-p
m <- n1*p
s <- sqrt(n1*p*q)
# define function to draw a plot
mean.histplot <- function(n,N=50000) {
  # n - sample size
    X <- matrix(rbinom(n*N,size=n1,prob = p),n,N)
    X <- colMeans(X)
    # generate histogram
    hist( X, breaks="Sturges", border="white", freq=FALSE,
            col="blue",
            xlab="Sample mean", ylab="",
            main=paste("Sample size =",n), axes=FALSE,
            font.main=1
        )
    box()
    axis(1)
    # plot N(mu,sigma/sqrt(n))
    lines( x <- seq(-30.0,30.0,.01), dnorm(x,m,s/sqrt(n)), 
    lwd=2, col="black", type="l"
    )
}
mean.histplot(1)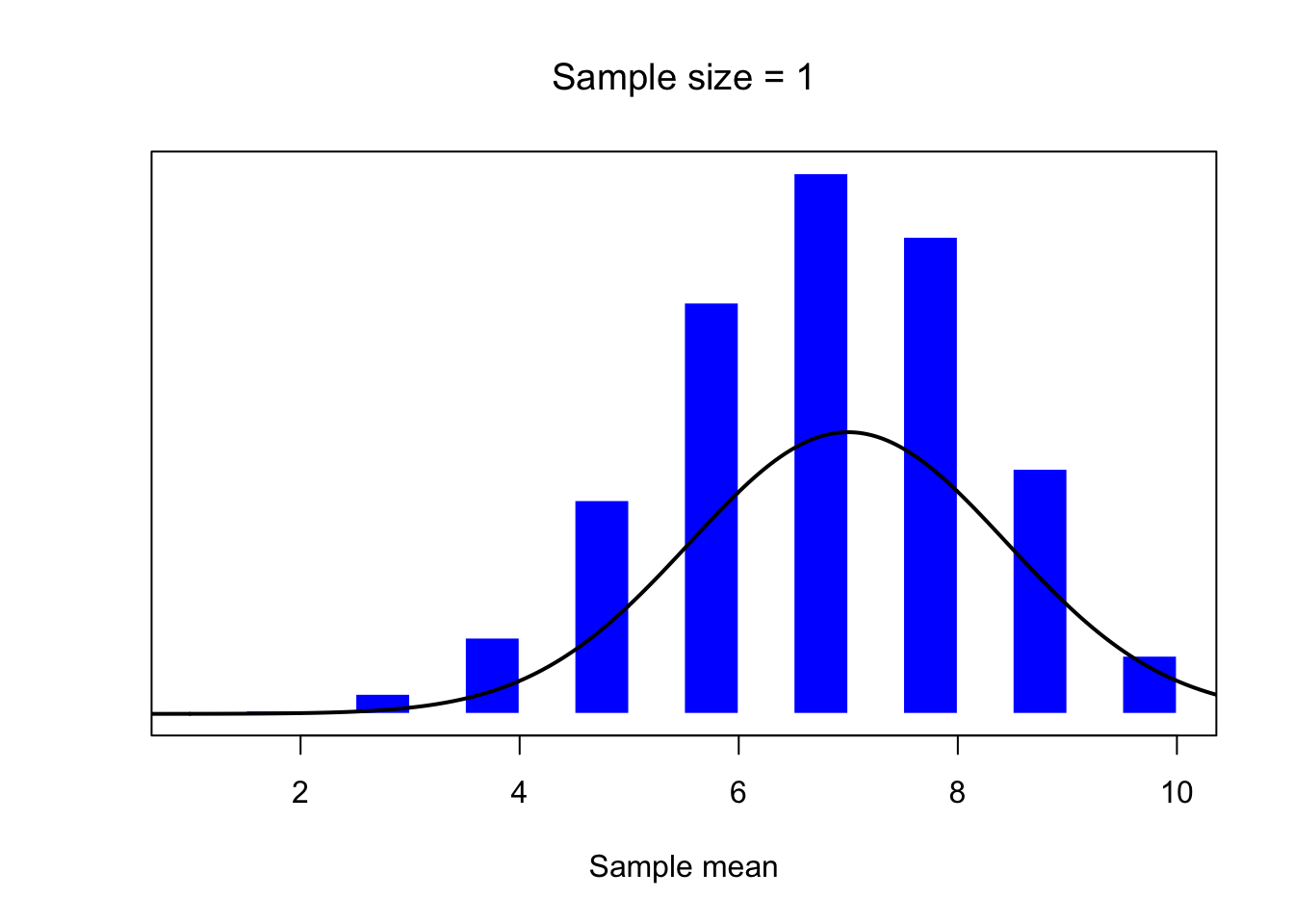

mean.histplot(4)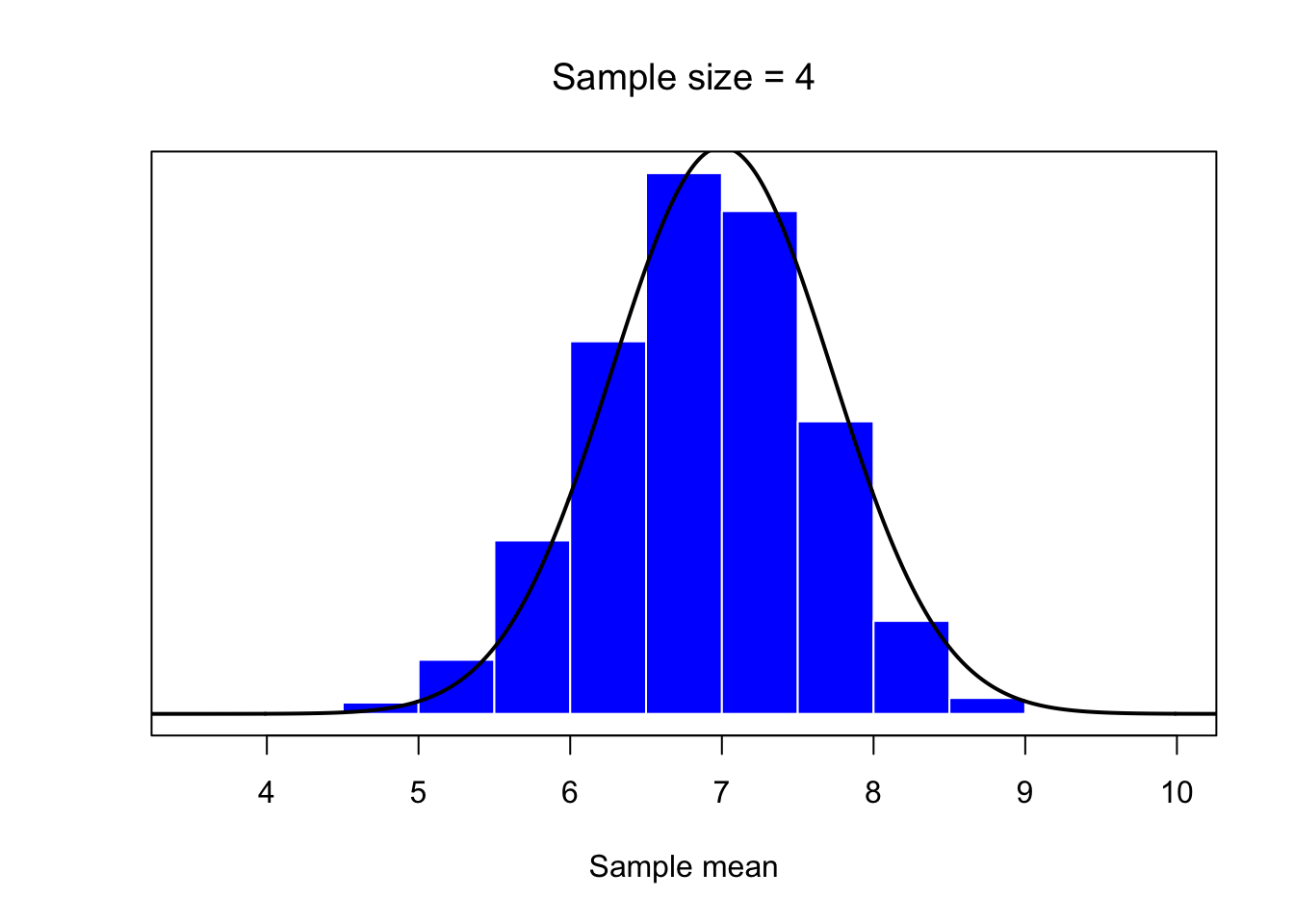

mean.histplot(30)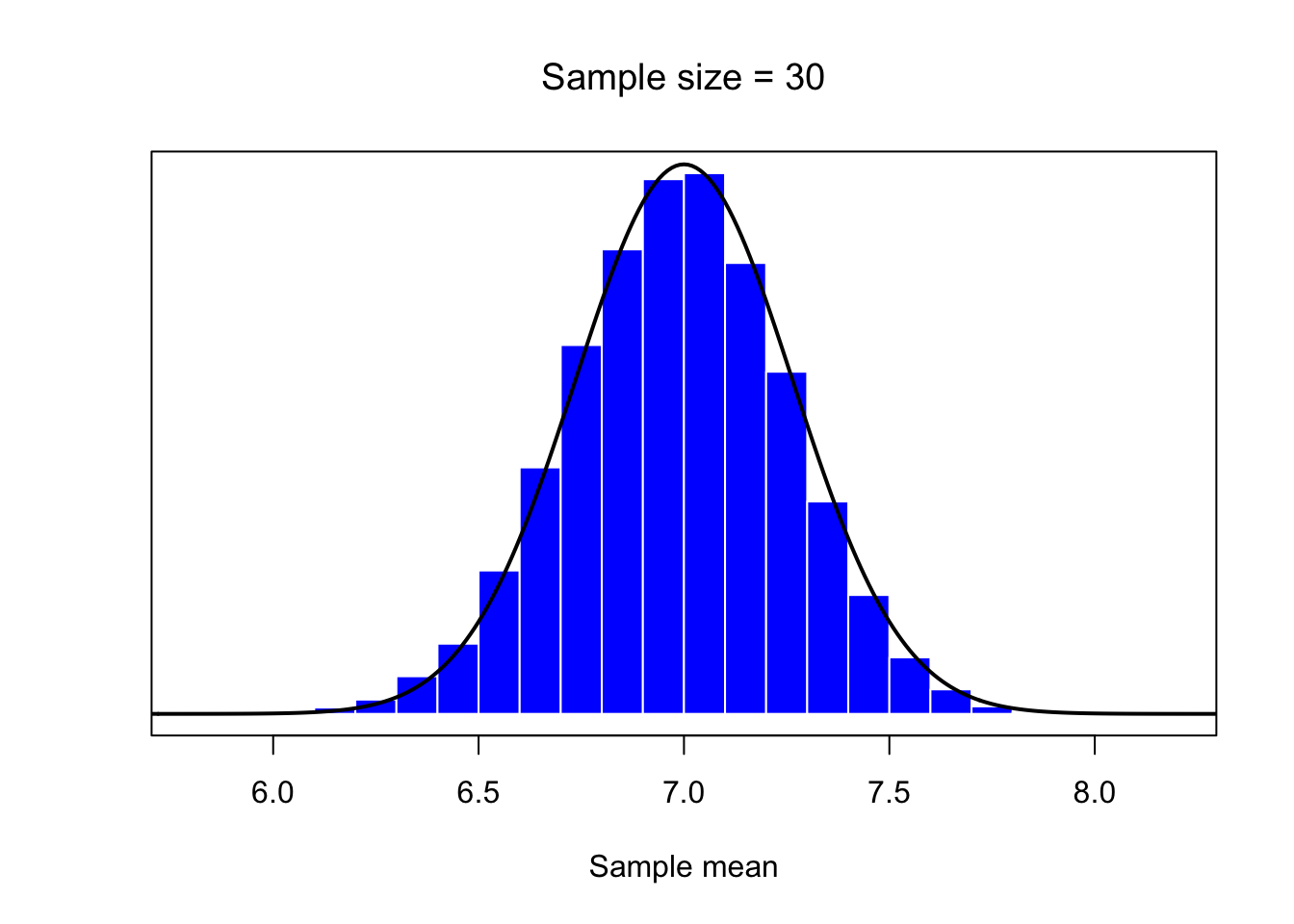

# parameters
n1<- 10
p <- 0.7
q <- 1-p
m <- n1*p
s <- sqrt(n1*p*q)
# define function to draw a plot
sample.mean <- function(n,N=50000) {
  # n - sample size
    X <- matrix(rbinom(n*N,size=n1,prob = p),n,N)
    X <- colMeans(X)
    return(X)
}
trace0 <- sample.mean(1)
trace1 <- sample.mean(4)
trace2 <- sample.mean(30)
library(plotly)

fig <- plot_ly(x = trace0, type = "histogram",name='Sample size = 1')
fig <- fig %>% add_histogram(x = ~trace1,name='Sample size = 4')
fig <- fig %>% add_histogram(x = ~trace2,name='Sample size = 30')
fig <- fig %>% layout(barmode = "overlay", xaxis = list(title = 'Sample mean'))
fig